Is The Rate Of Change The Same As The Slope
Rate of Change
Connecting Slope to Real Life
Why do nosotros need to find the slope of a line in real life?
The slope of a line tells u.s. how something changes over time. If nosotros find the slope nosotros tin find the rate of alter over that period.
This can be practical to many real life situations.
Take a await at the following graph.
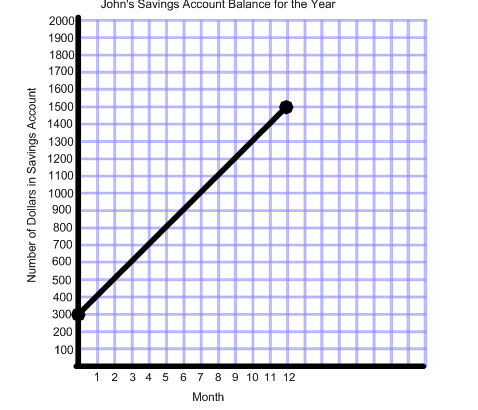
This graph shows how John's savings account balance has inverse over the form of a twelvemonth. We can see that he opened his account with $300 and by the end of the start month he had saved $100. Past the end of the 12 month fourth dimension span, John had $1500 in his savings account.
John may want to analyze his finances a trivial more and figure out about how much he was saving per month. This is called the rate of change per month.
By finding the slope of the line, we would exist calculating the rate of change.
We can't count the rise over the run like nosotros did in the calculating slope lesson because our units on the x and y axis are not the same. In nigh real life problems, your units will not be the same on the 10 and y axis. And then, nosotros need another method!
We will need to use a formula for finding slope given two points.
Gradient Formula
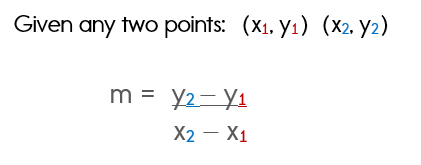
If y'all've never used this formula earlier, delight visit our page on using the slope formula.
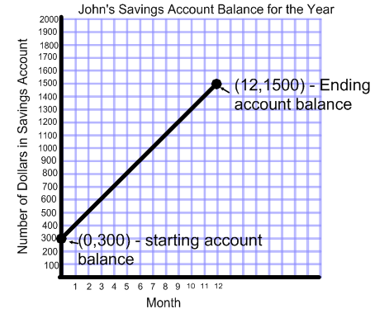
Let's take a look at John's graph again. John would like to find out how much money he saved per calendar month for the twelvemonth.
In other words, John wants to know the charge per unit of change per month. We are finding out how much John's account changes per month (on average).
Nosotros see that his starting balance is $300. On the graph, this point is (0,300)
His ending account residue (on month 12) is $1500. This indicate is (12, 1500).
Therefore, our two ordered pairs are (0,300) and (12, 1500).
We tin now use the gradient formula to find the slope of the line. The slope is the charge per unit of change from i month to the next.
Take a look at how this can exist solved.
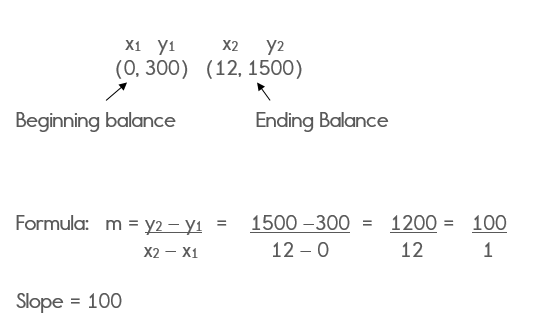
The gradient is equal to 100. This means that the charge per unit of modify is $100 per month.
Therefore, John saves on average, $100 per month for the year.
This gives u.s. an "overview" of John's savings per month.
Allow's take a await at another example that does not involve a graph.
Instance two: Rate of Change
In 1998, Linda purchased a house for $144,000. In 2009, the firm was worth $245,000. Find the average annual rate of change in dollars per yr in the value of the business firm. Circular your answer to the nearest dollar. (Let 10 = 0 represent 1990)
For this trouble, we don't have a graph to refer to in order to identify the two ordered pairs. Therefore, we must find two ordered pairs within the context of this problem.
I am given information most the year in which Linda purchased a house and the amount that the house is worth. Since these 2 items are related, I can write them as an ordered pair.
Special Note:
If time is involved (time of day, months, years...) information technology will always be your x coordinate!
Fourth dimension is always an x value.
Another affair that I would like to point out is the statement (Let x = 0 represent 1990)
*Believe it or not, mathematicians don't like to work with large numbers. So, instead of working with the bodily year, we are going to use a substitution. Information technology says, allow 10 = 0 stand for 1990. This is well-nigh likely the initial yr or the yr the firm was congenital.
The substitutions are as follows:
0 = 1990
1 = 1991
2 = 1992
iii = 1992
And then on...
Allow'south solve.
Solution
Let x = yr
Let y = corporeality
Pace one: Write 2 ordered pairs:
(eight, 144,000) (In 1998, she purchased the house for $144,000)
(xix, 245,000) (In 2009 (19 years subsequently 1990) the business firm is worth $245,000)
Stride 2: Utilise the slope formula to find the slope.
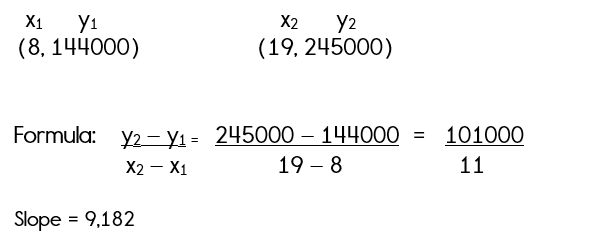
Linda's average annual rate of change if $nine,182 dollars per year.
This ways that on average, the value of her house increased by $nine,182 dollars per twelvemonth.
Now let'south have a look at i more example where all we are given is a graph. We must pay shut attention to the graph in club to solve the problem.
Allow's take a expect.
Instance 3: Analyzing a Graph to Make up one's mind Rate of Change
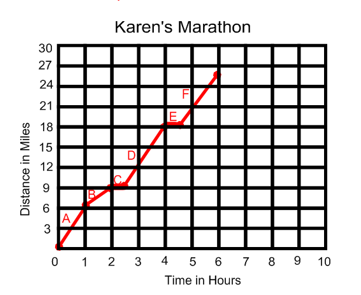
The following graph represents Karen's Marathon.
i. What is the rate of modify for interval A?
2. Explain what yous remember may have happened during interval C.
three. If the charge per unit of change for interval A had remained abiding throughout the whole marathon, how long would it accept taken Karen to end the marathon? (There are 26 miles in a marathon).
Solution
1. What is the rate of alter for interval A?
Find that interval is from the first to 1 60 minutes.
Pace 1: Identify the two points that cover interval A.
The start point is (0,0) and the second point is (1,vi).
Step 2: Use the slope formula to find the slope, which is the rate of change.
2. Explain what you lot think may have happened during interval C.
During interval C, Karen took a break and stopped running. During that i/2 hour time period, her distance did not increase.
iii. If the rate of change for interval A had remained constant throughout the whole marathon, how long would it have taken Karen to finish the marathon? (In that location are 26 miles in a marathon)
The 3 examples to a higher place demonstrated 3 different means that a rate of change problem may be presented.
But remember, that rate of change is a way of request for the slope in a existent world trouble. Real life problems are a piffling more challenging, but hopefully you now take a better understanding.
- Dwelling >
- Graphing Equations >
- Rate of Change
Need More Assistance With Your Algebra Studies?
Get access to hundreds of video examples and practise problems with your subscription!
Click hither for more information on our affordable subscription options.
Non ready to subscribe? Register for our FREE Pre-Algebra Refresher grade.
ALGEBRA Grade E-COURSE MEMBERS
Click here for more than data on our Algebra Class east-courses.
Need Help? Try This Online Estimator!
Chapter Products...
On this site, I recommend just one product that I apply and dear and that is Mathway If you brand a buy on this site, I may receive a small committee at no cost to you.
Source: https://www.algebra-class.com/rate-of-change.html
Posted by: milnelatim1936.blogspot.com
0 Response to "Is The Rate Of Change The Same As The Slope"
Post a Comment